HackASat2020 Quals Writeups

About Hackasat

Hackasat2020 Quals was a ctf that took place on the weekend of May 23rd. I wasn’t planning on doing it but then a buddy from the CTF team Cntr0llz invited me to participate with them (thanks :D!).

Its challenges were space-themed, which means the tasks we had to perform were related to problems scientists or astronauts may face. Because no one had any experience solving space related problems or anything on that line every challenge involved hours of research, testing and learning. Even though the two challenges I solved were in the “easy tier” in the ctf, they were still medium/hard-ish related to anything I had done in other competitions. Anyway, here are the writeups for Track the Sat and Where’s the Sat?

Track the Sat

Challenge description: “You’re in charge of controlling our hobbiest antenna. The antenna is controlled by two servos, one for azimuth and the other for elevation. Included is an example file from a previous control pattern. Track the satellite requested so we can see what it is broadcasting”

It also gives us a compressed examples file, which we can use to figure out what our answer needs to have. It contains challenge examples, their solutions, a list of Two-Line-Element-Sets (TLEs) and a README.txt :

Track-a-sat
===========

We have obtained access to the control system for a groundstation's satellite antenna. The azimuth and elevation motors are controlled by PWM signals from the controller. Given a satellite and the groundstation's location and time, we need to control the antenna to track the satellite. The motors accept duty cycles between 2457 and 7372, from 0 to 180 degrees. 

Some example control input logs were found on the system. They may be helpful to you to try to reproduce before you take control of the antenna. They seem to be in the format you need to provide. We also obtained a copy of the TLEs in use at this groundstation.

The biggest reason I struggled in this challenge was because most of the concepts I needed to apply were completely unknown to me (I had no idea what PWM signals or azimuth or a duty cycle was), so I had to research a lot about them in order to understand them.

When we connect to the challenge using netcat it asks for our ticket and then gives us this:

Track-a-sat control system
Latitude: 33.4487
Longitude: -94.0815
Satellite: ORBCOMM FM19
Start time GMT: 1586598368.85645
720 observations, one every 1 second
Waiting for your solution followed by a blank line...

It seems we are given a position for our groundstation antenna, a satellite name and a start time in a format that we later realize is a UNIX timestamp. After a lot of research we realize that we can track a satellite’s position based on a certain time + its orbit, which is determined by its respective TLE, and all that can be calculated using a python library called Skyfield. So we need to calculate the position the satellite is at for every second in the 720-second range the challenge asks us for, starting with the given UNIX timestamp. But how does this position translate to the answer we need to give? This was were I struggled the most during the challenge. Looking at the sample solutions, it seems we have to give the challenge the timestamp, followed by two duty cycles that relate to the azimuth and elevation of the satellite position. Research time!

Azimuth: “An azimuth is an angular measurement in a spherical coordinate system. The vector from an observer to a point of interest is projected perpendicularly onto a reference plane; the angle between the projected vector and a reference vector on the reference plane is called the azimuth.”

Turns out it’s simply a measurement system used to determine the relative position of a celestial object (or our satellite) in relation to an observer (or our groundstation antenna). The following image explains it accurately:

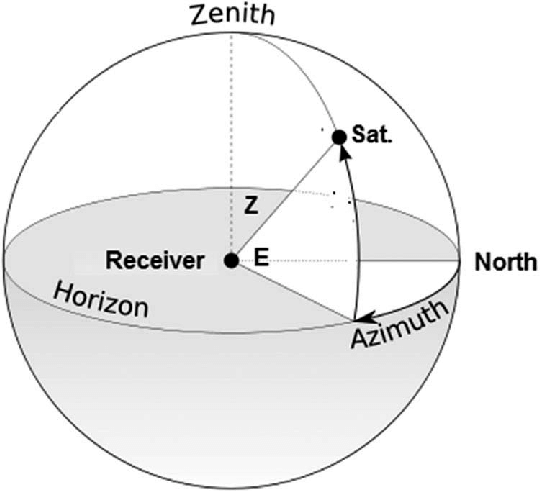
So we have to calculate the satellite’s azimuth coordinates and somehow translate them to a duty cycle. Lets first get started with our script to calculate the satellite’s azimuth coordinates.

from skyfield.api import EarthSatellite, Topos, load
from datetime import datetime

# TLE of our satellite (ORBCOMM FM19) found in the TLEs list (active.txt)
# We need it to generate a satellite object to determine its orbit
# and positions through time.
line1 = "1 25415U 98046C   20101.06884309  .00000044  00000-0  67064-4 0  9991"
line2 = "2 25415  44.9954 106.6270 0002985 215.4438 186.6131 14.32949120132262"

satellite = EarthSatellite(line1, line2)

# We have to convert the given timestamp to calendar format to be
# able to use it with the skyfield library
# (there are probably easier ways to do it, this is how I automated it)
timestamp = 1586598368.85645
everything = str(datetime.utcfromtimestamp(timestamp)).split(" ")
year = int(everything[0].split("-")[0])
month = int(everything[0].split("-")[1])
day = int(everything[0].split("-")[2])
hour = int(everything[1].split(":")[0])
minute = int(everything[1].split(":")[1])
second = float(everything[1].split(":")[2])

ts = load.timescale()
t = ts.utc(year, month, day, hour, minute, second)

# We have our satellite and our time ready to be combined
# The azimuth coordinates are determined from an observer reference frame,
# so we have to create an object to represent our observer.
# For that we enter a topocentric view by subtracting our satellite
# object with a topocentric object that represents our groundstation.

groundstation = Topos('33.4487 N', '94.0815 W') # These are the coordinates given
						# to us in the challenge

difference = satellite - groundstation
topocentric = difference.at(t)  

# Now we can finally get the azimuth coordinates of this topocentric object
# that represents the satellite position relative to our groundstation 
# at a time t

alt, az, distance = topocentric.altaz()
azimuth = az.degrees
altitude = alt.degrees
print("[Obj->Sat] Azimuth: (deg) " +  azimuth)
print("[Obj->Sat] Altitude: (deg) " + azimuth)

Running it, we get

[Obj->Sat] Azimuth: (deg) 296.059121239
[Obj->Sat] Altitude: (deg) 0.313248381751

The first part of our script is ready, we can calculate the azimuth coordinates of our satellite successfully. Now we have to figure out how to convert this coordinates to the actual duty cycles the antenna requires. After some thinking and reviewing the challenge instructions, we realize that we can convert the azimuth degree to a value between 0 and 180: north (usually 0°) and south (usually 180°) will both be 0°, and then grow clock-wise to 180°. After some more thinking we also realize that to convert this degree to a duty cycle value we can simply use the rule of 3. With 180° being our 100% (7273) and 0° being our 0% (2457), we can subtract those values to be able to apply the rule. We end up with the following math:

    if azimuth > 180:   # Reset to 0° when "reaching" South
        first = int((((azimuth - 180) *    (7372 - 2457)) / 180) + 2457)
#                            |                   |                 | 
# Degrees starting from South as 0°              |                 |
# Conversion to apply rule of 3 _________________|                 |
# Convert back to duty cycles value range _________________________|
    else:		# No changes in initial degree value since it didn't "reach" South
        first = int((((azimuth) * (7372 - 2457)) / 180) + 2457)
#			   |            |                  |
# Initial degree value ____|            |                  |
# Conversion to apply rule of 3 ________|                  |
# Convert back to duty cycles value range _________________|

With this we have the first two parts of what our answer should be figured out: the timestamps and the azimuth converted to duty cycles. We can test if our calculations are ok by running them with the information from the satellites in the given solutions and comparing.

The last number seems to act in a weird way. It doesn’t seem to relate to the azimuth coordinates’ altitude degrees in the same way the azimuth degrees relate to the first number. Looking at some of the solution samples we can see that there are points where the first duty cycle value goes from 2457 to 727x, which means that the azimuth degrees reached 0° or, in other words, South, and jumped to 180°, which makes complete sense. Now, what is weird here is that when the first duty cycle value makes the jump, the second one does too. This does not seem logical since the altitude is a completely independent variable from the azimuth degrees. Or at least that’s what I thought at first.

It is still odd to me that the duty cycles were calculated this way, but I will try to do my best to explain it with words (sorry, there’s just no way I’m designing a 3d model to explain this :/).

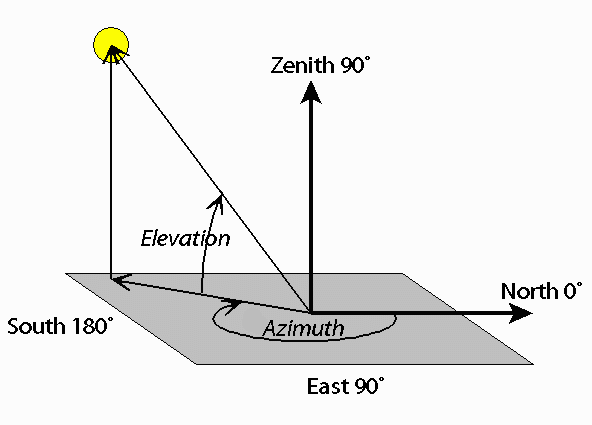
The azimuth elevation is normally an angle between 0 and 180, 0 - 90 meaning it is below the horizon and 90 - 180 meaning it is above the horizon. In the picture above we can see the elevation angle is of about 45° above the horizon, or 135° (90 + 45). Running our script with the sample satellites given to us in the challenge we can see that the elevation values always go from 0° to 90°, so we can assume that the satellites’ elevation was measured starting with the horizon and going up from there, not needing a range of 180° but only of 90°. Now, the weird behavior in the solution samples happen when the azimuth of the satellite reaches South or, in other words, goes to the West side of our plane. The elevation duty cycle jumps together with the azimuth duty cycle, so there must be some relation between them (which in reality is not logical). After a lot of thinking I realized that the elevation angle was being measured from the point respective to the current azimuth degree of the satellite, but always from the East side of our plane. This means that when the satellite’s azimuth was 179° in the East side of the plane the altitude would be measured as it usually is, not causing any weird behavior or weird duty cycle jumps, but when it crossed to the West side of the plane, the azimuth would jump to 0°, and the elevation would be calculated from the 0° point but on the East side instead of the West side of the plane, going all the way up to the zenith and then down to the actual position of the satellite. This might be hard to understand without having a look at it graphically, try to imagine it (I’m sorry I can’t provide you with graphical reference for this idea).

This theory would explain the jumps and weird behavior in the elevation duty cycles related to the azimuth of the satellite. After testing it with the sample solutions we realize that’s how it was being calculated. Now that we figured out the three values necessary for our solution to the challenge, we can just build a for loop to go through all the timestamps we need to present as a solution and then get pwntools in the game to interact with the remote instance of the challenge (we could also do this manually, but here’s the pwntools implementation anyway :D). The final script for the solution looks like this:

#!/usr/bin/env python3
# -*- coding: utf-8 -*-

from pwn import *
from skyfield.api import EarthSatellite, Topos, load
from datetime import datetime
from time import sleep # Just to make analyzing during runtime easier

final = ""
ticket = "REDACTED TICKET"

p = remote("trackthesat.satellitesabove.me", 5031)
p.recvuntil("please:")
p.sendline(ticket)
p.recvuntil("line...")

line1 = "1 25415U 98046C   20101.06884309  .00000044  00000-0  67064-4 0  9991"
line2 = "2 25415  44.9954 106.6270 0002985 215.4438 186.6131 14.32949120132262"


groundstation = Topos('33.4487 N', '94.0815 W')

satellite = EarthSatellite(line1, line2)

#timestamp = 1586789933.820023 # 0
timestamp = 1586598368.85645  # chall
a = int(str(timestamp).split(".")[0])  # Just some formatting for the timestamp for loop
b = "." + str(timestamp).split(".")[1]


for i in range(a, a + 720):
    i = float(str(i) + b)
    everything = str(datetime.utcfromtimestamp(i)).split(" ")
    year = int(everything[0].split("-")[0])
    month = int(everything[0].split("-")[1])
    day = int(everything[0].split("-")[2])
    hour = int(everything[1].split(":")[0])
    minute = int(everything[1].split(":")[1])
    second = float(everything[1].split(":")[2])
    ts = load.timescale()
    t = ts.utc(year, month, day, hour, minute, second)
    
    difference = satellite - groundstation
    topocentric = difference.at(t)
    alt, az, distance = topocentric.altaz()
    azimuth = az.degrees
    altitude = alt.degrees
    
    #print('[Obj->Sat] Azimuth: (deg)', azimuth)
    #print('[Obj->Sat] Altitude: (deg) ' + str(altitude))

    if azimuth > 180:
        first = int((((azimuth - 180) * (7372 - 2457)) / 180) + 2457)
        second = int((((90 + (90 - altitude)) * (7372 - 2457)) / 180) + 2457)
    else: 
        first = int((((azimuth) * (7372 - 2457)) / 180) + 2457)
        second = int((((altitude) * (7372 - 2457)) / 180) + 2457)

    #print("First: " + str(first))
    #print("Second: " + str(second) + "\n\n")
    
    entry = str(i) + ", " + str(first) + ", " + str(second) + "\n"
    #print(entry)
    
    final += entry
    
    #sleep(0.02)

final += "\n"
print(final)

p.sendline(final)
print(p.recvall())

With the final script done and the flag obtained, Track the Sat is finished.

Where’s the Sat?

This challenge was rather easy after all the research and skyfield documentation read for the previous challenge. Challenge description: “Let’s start with an easy one, I tell you where I’m looking at a satellite, you tell me where to look for it later.”

When we connect with netcat and provide our ticket we get this:

Please use the following time to find the correct satellite:(2020, 3, 18, 19, 18, 14.0)
Please use the following Earth Centered Inertial reference frame coordinates to find the satellite:[5408.543507363938, 2906.793258078781, -2834.1992918111864]
Current attempt:1
What is the X coordinate at the time of:(2020, 3, 18, 14, 10, 48.0)?

We have to provide it a satellite’s position at a given time.

We are given a list of satellites in the downloadable file stations.txt. It is a list of TLEs from which we can calculate each satellite’s orbit.

The challenge gives us the position the wanted satellite is at at a given time. Having this in mind, we can calculate every satellite’s position and that given time and look for a match to find the satellite wanted for the challenge.

We build a python script to do this:

from skyfield.api import EarthSatellite, Topos, load


f = open("./stations.txt", "r").read()
stations = f.strip().split("\n")

ts = load.timescale()
t = ts.utc(2020, 3, 18, 19, 18, 14.0)

for i in range(72):			# stations.txt has 72 TLEs
    name = stations[(3*(i+1)-3)]	# Get the satellite name for each TLE
    line1 = stations[(3*(i+1)-2)]	# Get the first line of each TLE
    line2 = stations[(3*(i+1)-1)]	# Get the second line of each TLE
    print("[Satellite Name]", name)	# Prints to debug if the information
    print("[Line 1]", line1)		# is correct
    print("[Line 2]", line2)


    satellite = EarthSatellite(line1, line2)	# We create a satellite object
    geocentric = satellite.at(t)		# from each TLE, and calculate its
    position = str(geocentric.position.km)	# geocentric position for the
						# given time

    if "5408" in position:  # filter for the position the wanted satellite was at
			    # at the given time
        print("SATELLITE FOUND: " + name + "\nPosition: " + position)
        break		    # break out of the loop when we find it

We run the script and get the wanted satellite:

SATELLITE FOUND: 1998-067PN              
Position: [ 5408.54350736  2906.79325808 -2834.19929181]

Having the wanted satellite we can calculate its position at any time using the satellite object we created inside our loop. This means we can keep our satellite object to use it to calculate the coordinates the challenge wants.

I was too lazy to apply pwntools here since taking the times from the challenge and formatting them into a usable format for the script would’ve been a waste of time, so I just did an input prompt and introduced the values from nc as I got them, getting the answers and pasting them back into nc to get the flag. Here’s the final version of the script:

#!/usr/bin/env python3
# -*- coding: utf-8 -*-

from skyfield.api import EarthSatellite, Topos, load

ticket = "REDACTED TICKET"

f = open("./stations.txt", "r").read()
stations = f.strip().split("\n")

ts = load.timescale()
t = ts.utc(2020, 3, 18, 19, 18, 14.0)

for i in range(72):
    name = stations[(3*(i+1)-3)]
    line1 = stations[(3*(i+1)-2)]
    line2 = stations[(3*(i+1)-1)]
    #print("[Satellite Name]", name)
    #print("[Line 1]", line1)
    #print("[Line 2]", line2)


    satellite = EarthSatellite(line1, line2)
    geocentric = satellite.at(t)
    position = str(geocentric.position.km)
    #print(str(str(geocentric.itrf_xyz()).split(" ")[1])[:-4] + "\n\n")
    #print(position + "\n\n")

    if "5408" in position:
        print("SATELLITE FOUND: " + name + "\nPosition: " + position)
        break


while True:
    timeinput = input("New Time: ").split(",")
    print(timeinput)

    newtime = ts.utc(int(timeinput[0]),int(timeinput[1]),int(timeinput[2]),int(timeinput[3]),int(timeinput[4]),float(timeinput[5]))
    newgeocentric = satellite.at(newtime)
    newposition = str(newgeocentric.position.km)
    print("Newposition: " + newposition)

And once more, with the final script done and the flag obtained, Where’s the Sat? is finished :D

Thanks for reading the writeup and I hope I managed to explain every step of what I did successfully, if you have any questions or want to contact me for some other reason you can use any of the socials linked here.